今回の実験
今回は光を検出するCdSフォトセルを2個使用し、2か所の光の強度の差を検出します。
■実験方法
1.以下の回路図をつくります。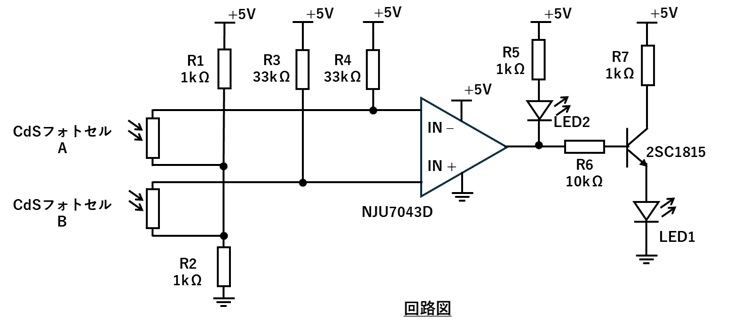
2.CdSフォトセルAとBにそれぞれの光の強さを変えたときに、LED1と2がどのように光るかを観察します。
■実験結果
1.以下のようにブレッドボード上に回路をつくりました。
2.それぞれのCdSフォトセルを指で光を遮るようにします。
まずはCdSフォトセルAの受光部に光があたらないように指で表面を覆いました。
LED1は消灯し、LED2が点灯しました。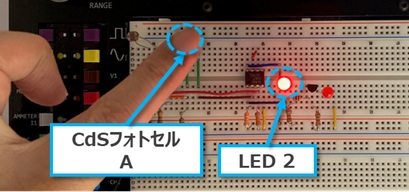
次にCdSフォトセルBの受光部に光があたらないように指で表面を覆いました。
LED1が点灯し、LED2は消灯しました。
<考察>
LEDの点灯と消灯の観察とともにオペアンプの出力電圧の変化から回路動作を考察しました。
今回のオペアンプはフィードバック回路ではありませんので、コンパレータと同様の動作と考えられます。
つまり、オペアンプ入力端IN-とIN+の電圧の比較となり、IN-の電圧が大きければ出力はグランド、入力端IN+の電圧が大きければ出力は電源電位になります。
CdSフォトセルAの光を遮った場合、オペアンプの出力は0.04V(≒グランド電位)でした。
CdSフォトセルBの光を遮った場合、オペアンプの出力は5.06V(≒電源電位)でした。
それぞれのオペアンプ入力端の電圧は、抵抗33kΩとCdSフォトセルの分圧回路ですので、CdSフォトセルの光を遮った場合、素子の抵抗が大きくなっていると考えられます。
LEDの動作については、以前の実験で記述していますね。
オペアンプの出力電位が低いとトランジスタのベース電位は低くオンしないのでLED2側の電流のみが流れます。
反対に出力電位が高いとLED2側には電流が流れないが、トランジスタはオンするためLED1側のみに電流が流れます。
今回の部材
CdSフォトセル MI527
CdS(硫化カドミウム)フォトセルは、当たる光の強さに応じて抵抗値が変化するCdSの性質を利用しています。
今回使用したMI527のデータシートによると、受光部に光が当たった場合の抵抗値は10k~20kΩでした。(10ルクスの場合を明抵抗として記載されています)
受光部の光を遮った場合の抵抗値は1MΩでした。(10ルクスの光を消してから10秒後の値を暗抵抗として記載されています)
カドミウムを含むCdSフォトセルは欧州RoHS指令などの規制対象になります。
代替技術の進化にともない例外規定は縮小され、シリコンフォトダイオードやフォトICなどへの代替が進んでいます。
今回の実験室
マイクロホンは音を電気信号に変換するデバイスです。
今回は音の違いを電気信号の違いとしてオシロスコープで観測します。
■実験方法
1.回路図1のようにマイクロホンとオペアンプの増幅回路を接続した回路をつくります。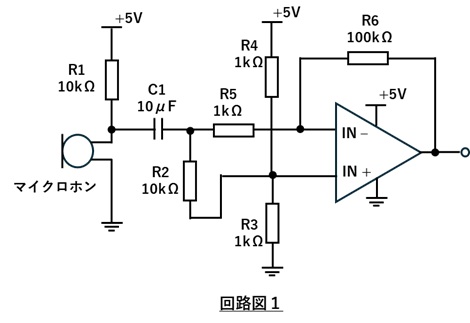
2.電源を入れ、マイクロホンに向かって声を出し、オシロスコープの波形を観察します。
「あ~」、「い~」、「う~」、「え~」、「お~」など異なる声を発音し、波形の違いを確認します。
■実験結果
1.回路図をブレッドボード上につくりました。
2.電源を入れ、マイクロホンに向かって「あ~」から「お~」まで発音したときの波形を観測しました。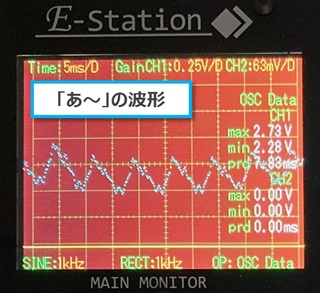
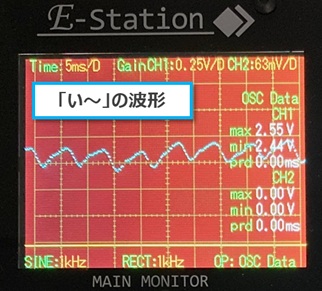

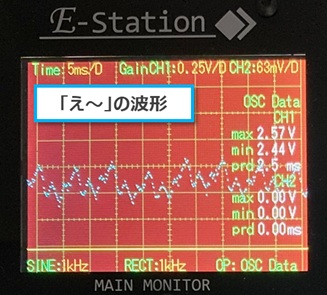

それぞれの波形を比較してみます。
いずれの波形も形は異なりますが、それぞれが繰り返しの波形になっています。
その繰り返し時間(波長)はほぼ同じくらいでした。
(=基本周波数はほぼ同じと考えられます)
それぞれの繰り返し波形の形は異なっています。
(=高調波成分が異なっていると考えられます)
■考察
回路図2のように、実験回路のオペアンプ出力にエミッタフォロワ回路とスピーカを接続し、収音した音をスピーカから出力してみました。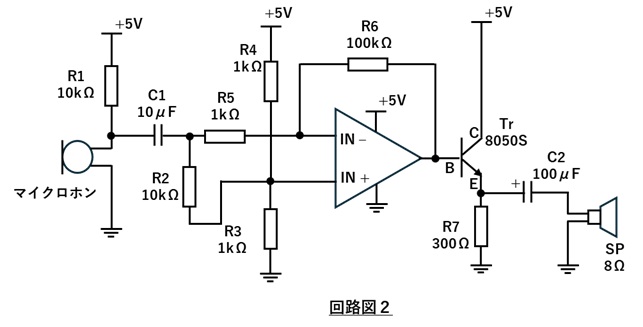
収音した音が、オペアンプの電圧増幅とエミッタフォロワの電流増幅でスピーカを駆動し音が再生されていることが確認できました。
その後、マイクロホンにセンサーケーブルを接続し、スピーカに近づけてみました。
マイクロホンとスピーカが接近すると、「ピー」という音が出力されその音の波形が正弦波に近いことが分かり、ハウリング現象が発生することも確認できました。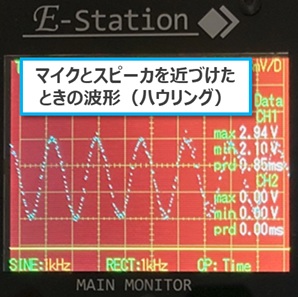
※ハウリングについて
ハウリングは、スピーカから出た音をマイクロホンが拾い、アンプで増幅しスピーカから再度出力されることが繰り返されること(正帰還)で発生します。
ハウリングは不快な音が出力されるだけでなく、アンプにもスピーカにも負荷がかかりますので長時間続けることは避ける必要があります。
ハウリングの対策には、マイクとスピーカの位置や角度を変えるような音響的な対策と、イコライザやハウリングサプレッサのような電気的な処理での対策でハウリングを抑制する方法があります。
今回の部材
マイクロホン
マイクロホンは、音声などの音を電気信号に変換する装置または部品です。
マイクロホンはいくつかの観点で分類されます。
ここでは変換原理や構造での分類と特性での分類を紹介します。
変換原理や構造で分類した場合、
・ダイナミック型
・ECM(エレクトレットコンデンサーマイク)型
・MEMS(微小電気機械システム)型
が使われます。
電子機器に組み込む場合、電源は必要としますが小型化が可能なECM型やMEMS型が使用されることが一般的です。
特性面もいくつかの分類方法がありますが、ここでは指向性に着目した分類を紹介します。
・無指向性(どの方向も同じ感度)
・単一指向性(前面の感度は高く、後方と側面は低い)
・双指向性(前面と後方は感度が高く、側面の感度が低い)
・狭指向性(特定の方向のみ感度が高い)
このようにマイクロホンはいろんな種類がありますので、用途に応じて選ぶことが重要です。



平素は格別のご高配を賜り、厚く御礼申し上げます。
令和7年11月19日(水)~21日(金)にパシフィコ横浜にて
EdgeTech+2025 の「IDEC横浜パビリオン」に出展しております。
お近くにお越しの際は、是非弊社のブースにもお立ち寄りください。
心よりお待ち申し上げております。


今回の実験
今回は前回のエミッタ接地増幅回路を使って、スピーカーから音を出力します。
またその際に考慮すべき点を考察します。
■実験方法
1.以下の回路図のように前回のエミッタ接地増幅回路を使い、トランジスタのコレクタに
100μFのコンデンサを介してスピーカーを接続します。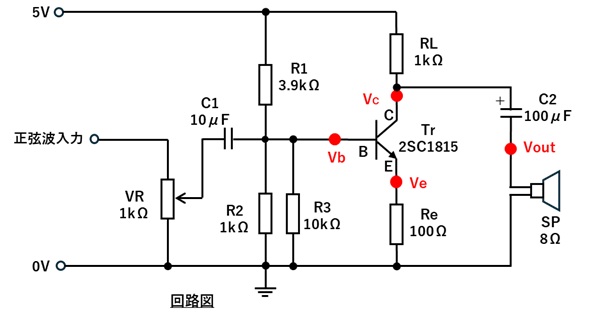
2.いったんスピーカーの片側をはずし(Vout端子オープン)、入力信号に正弦波1kHzを入力します。
その後、コレクタ電圧が2.5Vp-p程度になるように半固定抵抗器VRを調整します。
3.スピーカー端子を接続し、スピーカーからの発音状態とコレクタ電圧Vcの波形を観察します。
4.以下のように抵抗を変更し、同様にスピーカーからの発音状態とコレクタVcの波形を観察します。
Re:100Ω→10Ω 、 RL:1kΩ→100Ω
(実験回路の電圧増幅率はRL/Reです。同じ比率の抵抗値変更ですので電圧増幅率は
同じ結果が得られると想定できます。今回はその正しさを確認します。
厳密には抵抗値の変更で動作点も変化しますが、今回は考慮せずに進めます。)
■実験結果
1.以下のようにブレッドボード上に回路をつくりました。
2.実験方法2に従って、スピーカー端子の片側の接続を外し、1kHz信号を入力後に
半固定抵抗器を調整し約2.5Vp-pに合わせました。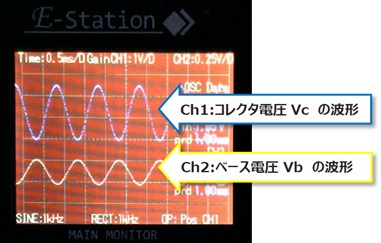
3.実験方法3に従ってスピーカー端子を接続し、スピーカーの発音状態と波形を確認しました。
スピーカーからは、小さな音が鳴っていることが確認できました。
コレクタ電圧Vcの波形は、実験方法2と比べかなり正弦波が小さくなっていることが分かりました。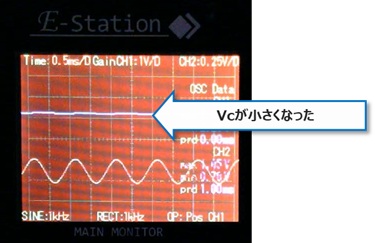
4.実験方法4に従って抵抗ReとRLを変更し、スピーカーの発音状態と波形を確認しました。
スピーカーの音が実験方法3と比べて少し大きくなることが分かりました。
また、コレクタ電圧Vcの正弦波も少し大きくなっていることが分かりました。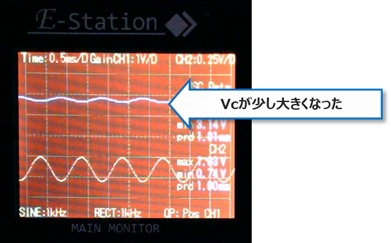
<考察>
今回の回路でスピーカーを駆動し発音できることが分かりました。
しかし、音は小さく、また同じ電圧増幅率であっても異なる結果になりました。
出力段の電流を考察してみます。
電源から供給される電流は図1のように抵抗RLを通ったあとに2つに分かれます。
前回実験から電流はバイアス電流(直流)と正弦波が増幅された電流(交流)が足し合わさったものになります。
コンデンサC2がありますので、直流成分はスピーカー側へは流れません。そのため、直流成分であるバイアス電流はすべてトランジスタ側に流れます。(動作点は変わらない)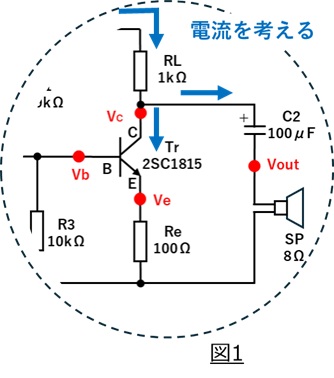
一方で、交流成分を考えます。
コンデンサC2の1kHzのインピーダンスは約1.6Ω程度になります。そのため図2のように交流信号は抵抗RLを通じてスピーカーに供給されることになります。
抵抗RLは1kΩですので、抵抗分割の結果、スピーカー側の電圧は小さくなることが分かります。
つまり、回路にスピーカーを接続した場合、内部抵抗の大きな交流信号源に小さな負荷抵抗をつないだことと同じような状況になります。
実験方法4でRLとReをそれぞれ小さい値に変更すると、スピーカーの音が大きくなりました。これもこの関係から理解できますね。(交流信号源の内部抵抗を小さくしたことと同じ)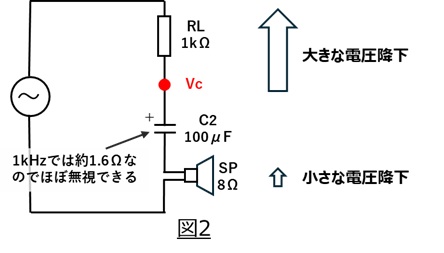
今回はエミッタ接地増幅回路で直接スピーカーを鳴らしました。
しかし、実験結果からわかるように、エミッタ接地増幅回路は電圧増幅に適していますが、低いインピーダンス(≒重たい負荷)の駆動には向いていません。
スピーカーのような低いインピーダンスのものを駆動する場合は、エミッタ増幅回路の後段にエミッタフォロワ回路を入れることでしっかり駆動できるようになります。
今回の実験部材
スピーカー
スピーカーは電気信号を振動に変換することで、耳や身体で感じる音をつくり出す装置です。
音楽信号などは複数の周波数の電気信号で表すことができ、それをアンプで増幅しスピーカーに送られ音を発します。
スピーカー内のコイル(銅線やアルミ線を巻いたもの)に電流が流れると、磁石の磁界によるフレミングの左手の法則で力が発生し、コイルに機械的に固定されている振動板(紙やプラスチックなどで円錐状のものが多い)を動かします。 振動板が前後に動くことで空気を圧縮し音が発生します。
スピーカーの振動板の前後は逆の位相の音が出ていることになりますので、そのままでは前後の音を打ち消してしまいます。そのため、スピーカーは木製やプラスチックの箱(エンクロージャー)に取り付けるのが一般的です。 エンクロージャーには密閉型やバスレフ型など目指す音に合わせていろんな方式があります。
今回の実験
前回の「BJT増幅回路の原理」では、シンプルなエミッタ接地増幅回路の直流動作を観測することで増幅原理を学びました。
増幅回路は交流信号を増幅することが主目的ですので、今回は標準的なエミッタ接地増幅回路で交流波形を観測し増幅動作の理解を深めます。
実験の前に、以下の図をもとに前回と今回の違いを整理してから始めたいと思います。
前回はベース電圧Vbとコレクタ電圧Vcの直流電位の変化をプロットしました。これによりVbの変化に対してVcが大きく変化(≒増幅)することが分かりました。
今回は前回の回路をもとに、より実用的な回路で実験します。
前回からの主な変更点は以下です。
①抵抗分割を使ってベース電圧に直流電位を与えます。
これは増幅回路の動作点を固定する目的です。バイアスを与えるとも言います。
(今回の電源電圧は+5Vですので0~5Vの範囲を超えての増幅はできません。
そのため交流を増幅する場合、交流的な基準(=動作点)をどこに設定するかを
決める必要があります。)
②コンデンサを通じて交流信号である正弦波をベース電圧に重畳します。
これによりコレクタ電圧から増幅された信号がでてくるか?を確認します。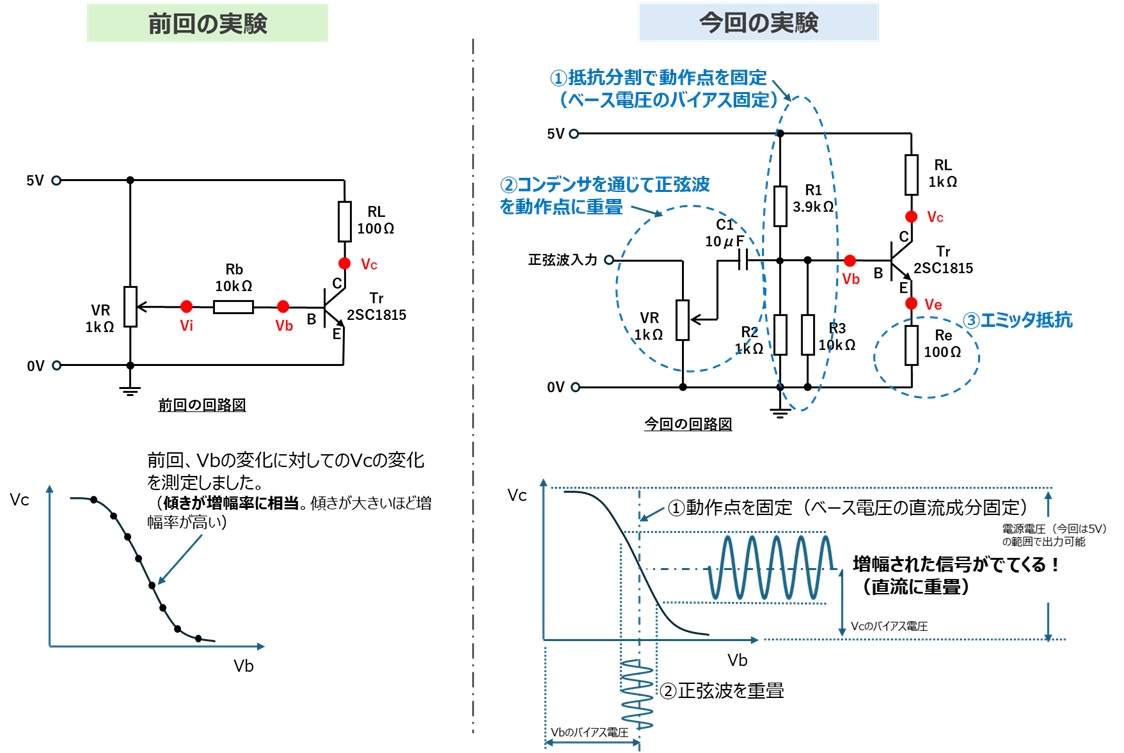
※今回の実験回路では、上記の変更点に加えて
③エミッタとグランド間に抵抗(以降、エミッタ抵抗と呼ぶ)を入れています。
このエミッタ抵抗は負帰還の役割を果たし回路を安定化させる効果があるため、
実用的なエミッタ接地増幅回路では組み込むことが一般的です。
エミッタ抵抗の役割は考察の後半で深堀します。
■実験方法
1.以下の回路図をブレッドボード上につくります。 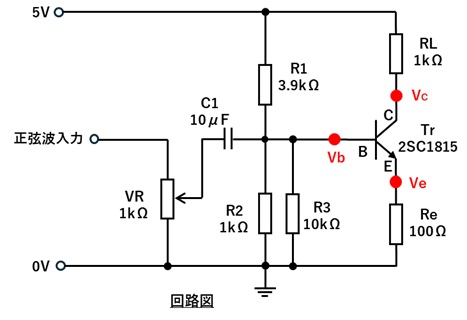
2.半固定抵抗器を左いっぱいに回し正弦波信号を入力しない状態で、ベース電圧Vb、
エミッタ電圧Ve、コレクタ電圧Vcを測定します。
3.入力端子に正弦波信号1kHzを入力し、半固定抵抗器をゆっくり右に回し、
ベース電圧Vbとコレクタ電圧Vcの波形をオシロで観測します。
4.正弦波信号を100Hz、10kHzに変更し、それぞれの信号での波形の変化を観測します。
5.波形の観測や電圧の測定結果から考察します。
■実験結果
1.以下のようにブレッドボードに回路をつくりました。
2.実験方法2の各直流電圧は以下の測定結果となりました。
3.実験方法3でのオシロの観測波形は図1のようになりました。
ベース電圧Vbとコレクタ電圧Vcの波形が上下反転していることが分かりました。
これはVb-Vc特性が負の傾きであるためです。(詳細は前回実験参照)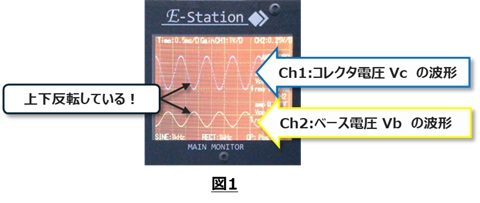
半固定抵抗器を右に回していくと、図2から図3のようにベース電圧Vbが大きくなるとともにコレクタ電圧Vcが大きくなることが観測できました。
さらにベース電圧Vbを大きくしていくと、図4のようにコレクタ電圧の下側の波形がクリップする(つぶれる)ことが分かりました。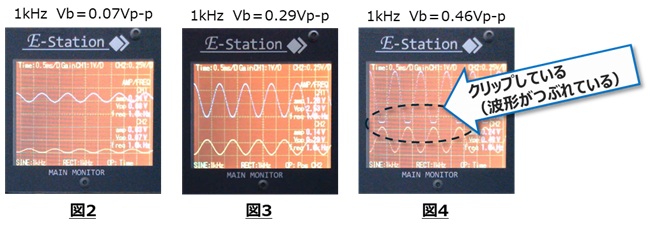
4.実験方法4に従って正弦波信号を100Hz、10kHzに変更し波形を観測しました。
図5~図7のように周波数を変更してもコレクタ電圧の振幅は変わらないことを
確認しました。(増幅率の周波数特性はほぼフラットであることが分かりました)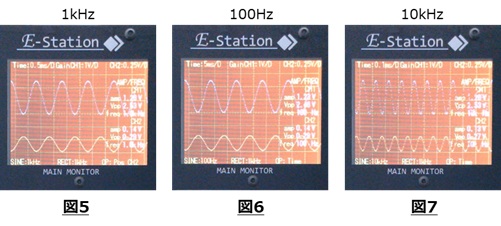
5.考察します
<コレクタ電圧Vcの波形クリップを考察>
実験方法3で入力電圧を大きくすると、図4のようにコレクタ電圧波形の下側がクリップしました。
クリップ波形を考察するために、前回実験と同様に今回の実験回路でのベース電圧Vbとコレクタ電圧Vcの直流特性を測定し、実験方法2で測定した動作点をプロットしました。(図8)
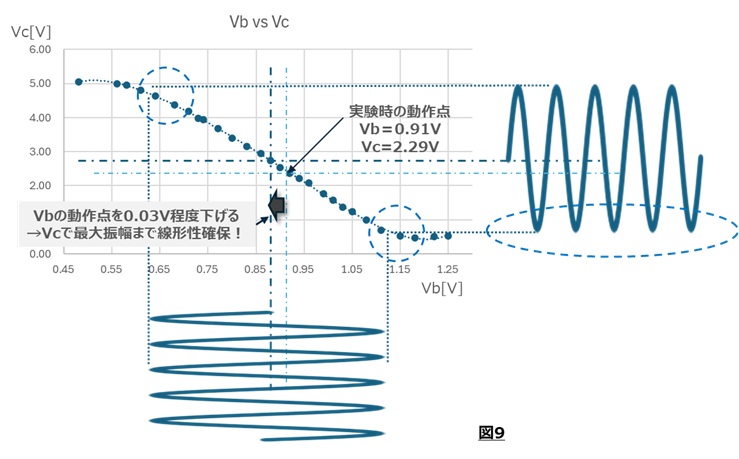
そのベース電圧の動作点に0.46Vp-pの信号を加えると、コレクタ電圧の下側は線形部分を超えてクリップすることが分かります。 上側波形がクリップしていないのはまだ線形の範囲のためであることも分かりました。
クリップしにくくするためには、Vbの動作点をVcの線形性が保てる中心に設計するのがよいですね。 今回の例では図9のようにVbの動作点をもう少し低い電圧に設定するとよいと思われます。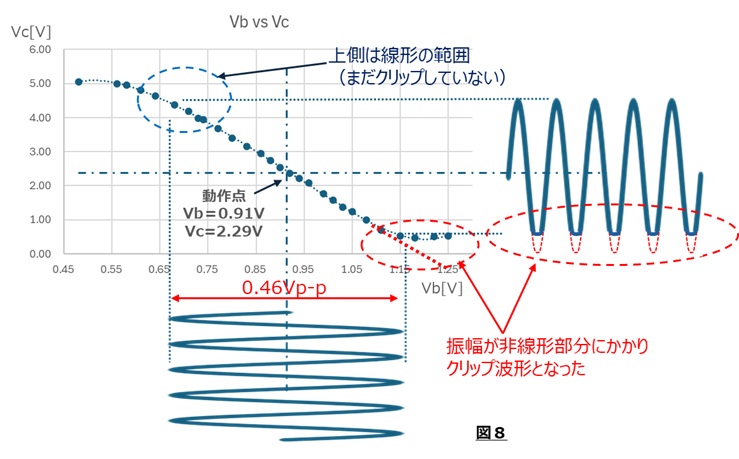
<エミッタ抵抗の考察>
冒頭でエミッタ抵抗が負帰還の役割を果たすと記しました。その負帰還動作のイメージを図10に記載しました。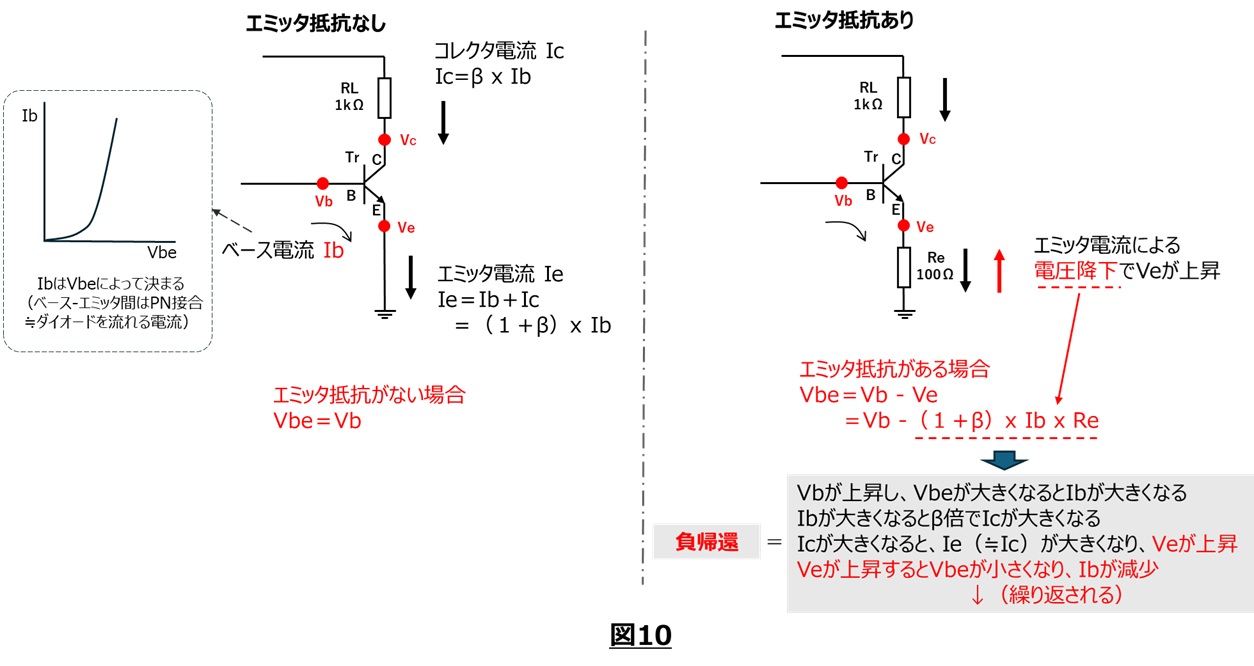
以下、エミッタ抵抗の負帰還がどのように特性に影響するかを増幅率で検証しました。
図13と図14のように、エミッタ抵抗を入れることで増幅率は低下しますが、横軸の入力電圧に対しての増幅率の変化は小さくなっており、入力信号に対する出力の線形性(直線性)が高まっていることが読み取れます。(理想は増幅率一定)
この線形性が高いということは、入力波形に対して出力波形が変化しにくい(歪が小さい)ということになります。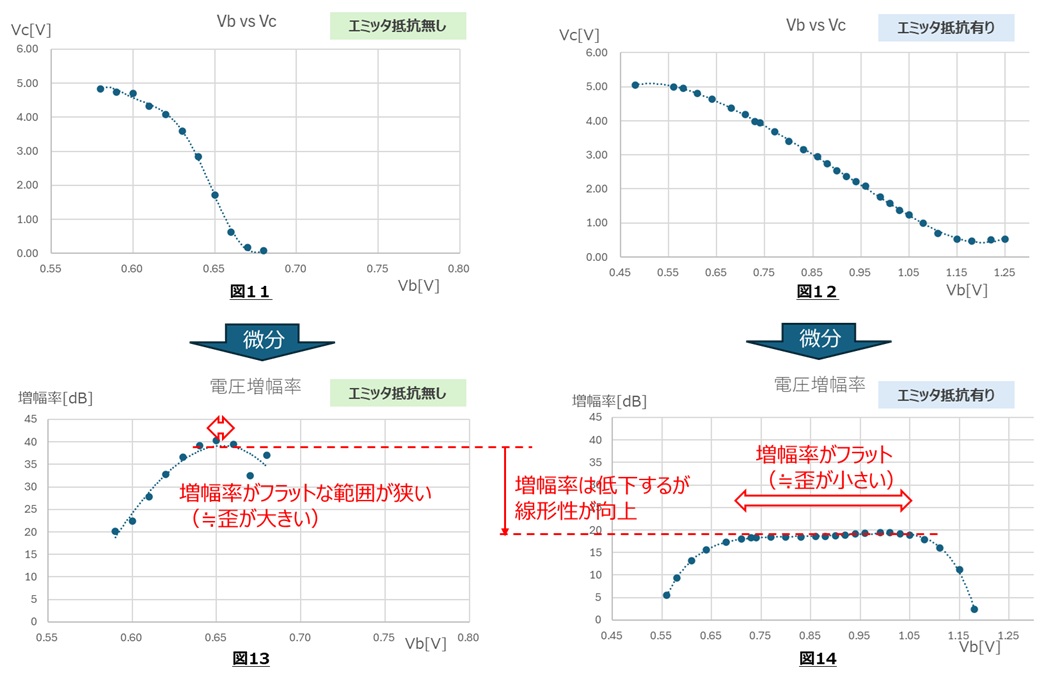
エミッタ抵抗による負帰還の効果は、上記のような線形性の改善による歪の低減以外にも以下のようなメリットがあります。
・熱安定性の向上(トランジスタ自体の電流増幅率の熱変化を吸収)
・増幅率のばらつき低減(エミッタ抵抗がない場合はトランジスタ自体の増幅率が支配的で、そのトランジスタの増幅率はばらつきが大きい。 エミッタ抵抗を入れた場合の増幅率≒RL/Reとなり、抵抗値で決定できる。 ※今回の回路では、増幅率RL/Re = 1kΩ/100Ω = 10倍 ≒ 20dB)
以上のような効果から、エミッタ接地増幅回路ではエミッタ抵抗を入れることが一般的です
今回の実験
BJT(バイポーラトランジスタ)を使った増幅回路の原理を実際に測定して勉強します。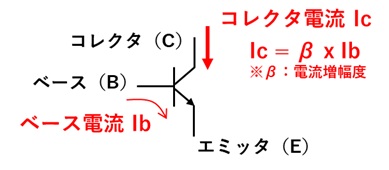
BJTの増幅原理はベース電流Ibに対して電流増幅率βに比例したコレクタ電流Icが流れることでした。
今回は原理の確認のためエミッタ接地回路を直流で動作させ、ベース電流に対してコレクタ電流の変化(電流増幅に相当)、ベース電圧に対してのコレクタ電圧の変化(電圧増幅に相当)を測定し動作を検証します。
※交流動作については次回確認します
■実験方法
1.以下の回路図をブレッドボード上につくります。
※エミッタをグランド側に接続するためエミッタ接地回路と呼びます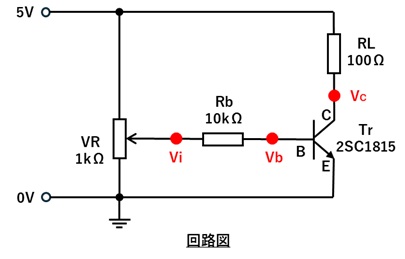
2.半固定抵抗器VRを調整し、ベース電圧Vbを0.58V~0.8Vまで0.01Vステップ程度で変化させます。
その際にベース電圧Vbの変化とともに、半固定抵抗端電圧Viとコレクタ電圧Vcを記録します。
抵抗Rbを流れるベース電流Ibと抵抗RLを流れるコレクタ電流Icを以下の式から求めます。
また、求めた各電流値から電流増幅率βを求めます。
(参考:電流増幅率はトランジスタ仕様書ではhFEと記載されています)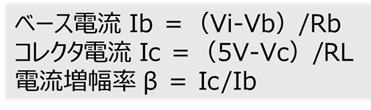
3.抵抗RLを100Ωから1kΩに変更し、実験方法2と同様に測定および計算を行います。
4.測定結果をグラフにまとめて考察します。
■実験結果
1.実験回路を以下のように準備しました。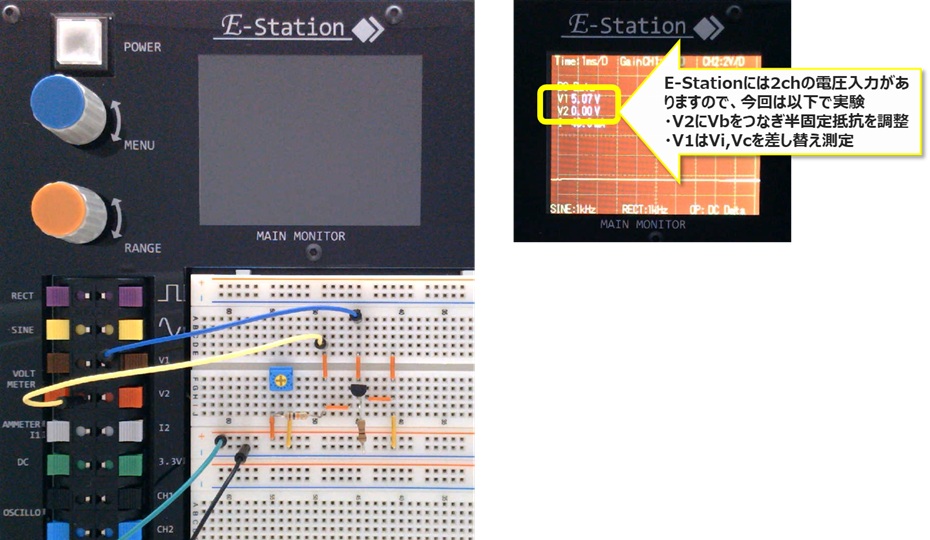
2.実験方法2および3の手順で抵抗RL=100Ωと1kΩのときの各電圧の測定と電流を計算しました。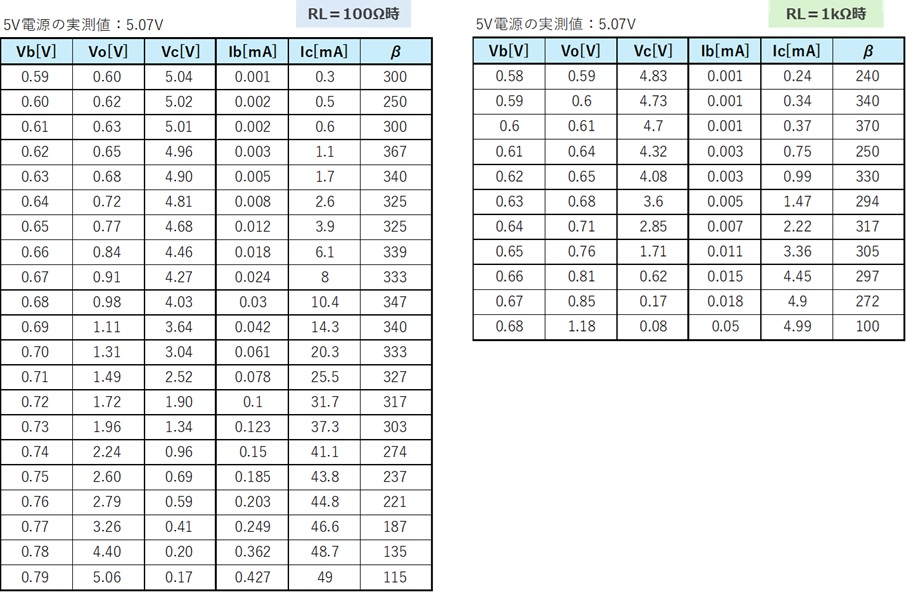
3.実験方法4にしたがって上記の測定結果を以下のグラフにまとめてみました。
上のグラフ:ベース電圧対コレクタ電圧、 下のグラフ:コレクタ電流に対する電流増幅率
左のグラフ:RL=100Ω、 右のグラフ:RL=1kΩ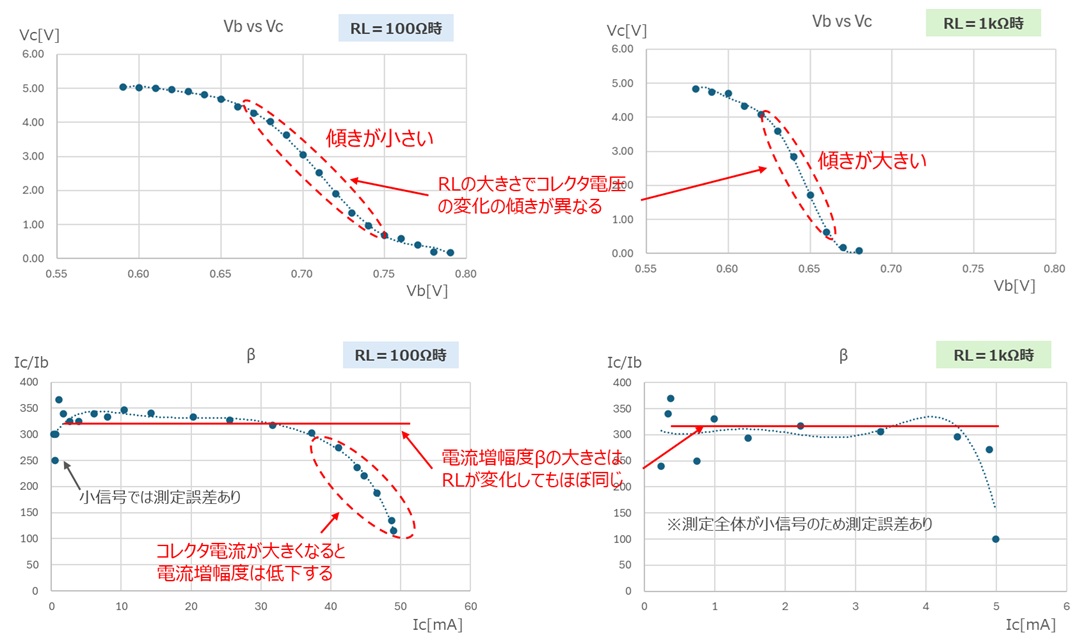
上のグラフはベース電圧に対してのコレクタ電圧の変化を表しています。
したがって傾きの大きさが電圧増幅率を意味しています。
(例えば左のRL=100Ωの図の場合、Vb=0.7Vを中心に0.02V変化させたとすると、Vcは3Vを中心に1Vくらい変化することになります。 つまりVbに対してVcは50倍変化していることになりますね。 参考ですが、この説明のような動作させる中心を動作点と呼びます。)
この図は負の傾きなのでイメージしにくいですが、傾きが負ということはベース電圧が大きくなるとコレクタ電圧は小さくなるということなので、交流で考えると位相が反転していることになりますね。
※位相が反転するのは回路図から予想できます。コレクタ電圧Vcは以下の式となります。![]() これはコレクタ電流が大きくなると、抵抗RLでの電圧降下が大きくなりVcが低下することを意味します。 つまりIbやIcが増加するとVcは低下するという逆の動きなので位相が反転しているということですね。
これはコレクタ電流が大きくなると、抵抗RLでの電圧降下が大きくなりVcが低下することを意味します。 つまりIbやIcが増加するとVcは低下するという逆の動きなので位相が反転しているということですね。
一方で、下のグラフはベース電流とコレクタ電流の比である電流増幅率βです。
ベース電流は非常に小さいので、測定誤差の影響を受けていますが、概ねコレクタ電流が変化しても一定(グラフでは水平)、かつ抵抗RLを変えても概ね同じ値であることが分かります。
※今回のトランジスタではβは310程度でした。 電流増幅率が一定ということでトランジスタが電流増幅の機能を果たしていることが確認できました。 ただ、コレクタ電流を大きくするとβが低下するため、電流増幅には限界があることも分かりました。
もう少し上側のベース電圧対コレクタ電圧のグラフの深堀りをしました。
傾きが電圧増幅率になりますので、上記のグラフを微分すれば電圧増幅率のグラフを描くことができます。 今回は多項式近似で関係式をもとめ微分計算しその結果をプロットしてみました。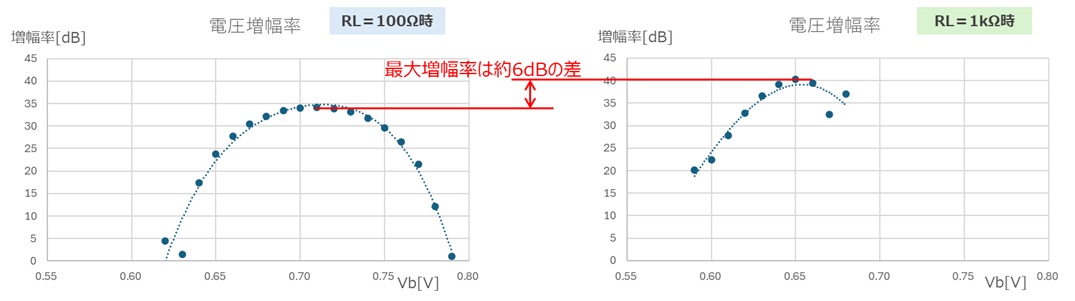 動作点(ベース電圧Vbやベース電流Ibをどこに設定するか)により電圧増幅率が変化しています。また抵抗RLが大きい方が電圧増幅率が高いことも分かりました。
動作点(ベース電圧Vbやベース電流Ibをどこに設定するか)により電圧増幅率が変化しています。また抵抗RLが大きい方が電圧増幅率が高いことも分かりました。
今回の測定では最大増幅率は6dB程度の差なので、RL=1kΩ時とRL=100Ω時のそれぞれの回路に同じ入力電圧を加えた場合のコレクタ電圧は、RL=1kΩ時が2倍くらい大きくなります。
※電圧の2倍をdB表示にすると、20xLog(2倍)≒6dBになります
今回の実験部材
バイポーラトランジスタ
バイポーラトランジスタとは、トランジスタの一種で、半導体のpn接合によって構成されたトランジスタのことです。
一般的に「トランジスタ」といえばバイポーラトランジスタを指していることも多いです。
バイポーラトランジスタには、ベース、エミッタ、コレクタの3つの端子がついています。ベースに流れる電流に応じてコレクタに電流が流れることを利用して回路を構成します。
(ベースに電流が流れると、コレクタはそれに応じて電源から電流を持ってくるイメージ)
バイポーラトランジスタにはpn接合の構造によってnpn型とpnp型に分けられます。npn型とpnp型は電流の流れる方向が逆になります。
バイポーラトランジスタは回路構成で電圧増幅にも電流増幅にも活用でき、また生産コストも安価であることから、多くの電子回路に利用されています。
なお、バイポーラトランジスタは電子と正孔の2種類のキャリアを持つため、2つを意味するバイの名がついています。 これに対して電界効果トランジスタ(FET)は電子か正孔のいずれか1種類を扱うので、ひとつを意味するユニを使いユニポーラトランジスタとも呼ばれます。

平素は格別のご高配を賜り、厚く御礼申し上げます。来る11/19(水)~21(金)にパシフィコ横浜で開催されます EdgeTech+2025 の「IDEC横浜パビリオン」に出展いたします。
会場では、電気・電子回路の基礎が学べる教育キット「E-Station」をご紹介させて頂きます。
是非この機会にご来場いただき弊社ブースへお立ち寄りくださいますようお願いいたします。
また、お知り合いの方々をお誘い合せの上、皆様でご来場ください。
心よりお待ち申し上げております。

━【 来場無料|事前登録制 】━━━━━━━━━━━━━━━━━━━━━━━━
下記URLより登録をお願いいたします。
来場登録受付中 ⇒ https://www.jasa.or.jp/expo/
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
▼最新情報は公式サイトから
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
公式サイト ≫ https://www.jasa.or.jp/expo/
参加企業・団体一覧 ≫ https://go.f2ff.jp/et25exhinomemail1006j
セミナー一覧 ≫ https://go.f2ff.jp/et25ttnomemail1006j


今回の実験
今回はコンデンサに電荷が蓄えられていく過程や電荷を放出していく過程を観測します。
■実験方法
1.図のように、コンデンサCと抵抗Rとプッシュスイッチ2個をブレッドボード上に配線します。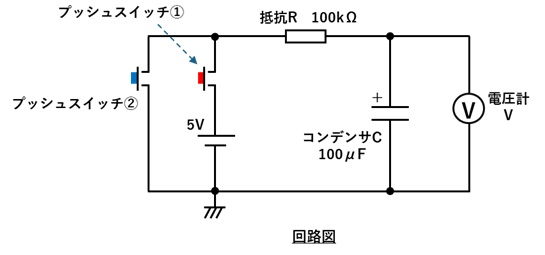
2.電源を投入し、プッシュスイッチ②のみを押し、コンデンサCの電圧を0Vにします。
3.プッシュスイッチ②を離しプッシュスイッチ①を押すと、5V電源から抵抗Rを通りコンデンサCに
電荷が供給されコンデンサCの電圧が上昇し、電圧計Vの表示が5Vに近づいていくことを
観察します。
4.プッシュスイッチ①を離しプッシュスイッチ②を押すと、逆にコンデンサCの電荷は抵抗を通じて
放出されコンデンサCの電圧は低下し、電圧計Vの表示が0Vに近づいていくことを観察します。
5.抵抗Rを10kΩ・1kΩに変更、またコンデンサCを10μF・1μFに変更し、上記の2~4を同様に
行い電圧計Vの変化を観察します。
6.電圧計Vを5Vにしプッシュスイッチ①②を押さない状態で電圧値を観測します。
■実験結果
・実験方法1~4を実施します。 プッシュスイッチ①を押すと電圧計Vの表示が増加し、プッシュスイッチ②を押すと電圧計Vの表示が減少していくことが確認できました。
増加と減少の傾きは一定ではなく、それぞれ増加時は5Vに近づくと緩やかに、減少時は0Vに近づくと緩やかになることが分かりました。
接続状態
プッシュボタンを押した状態
・実験方法5の抵抗とコンデンサの値を変化させると以下のような違いが分かりました。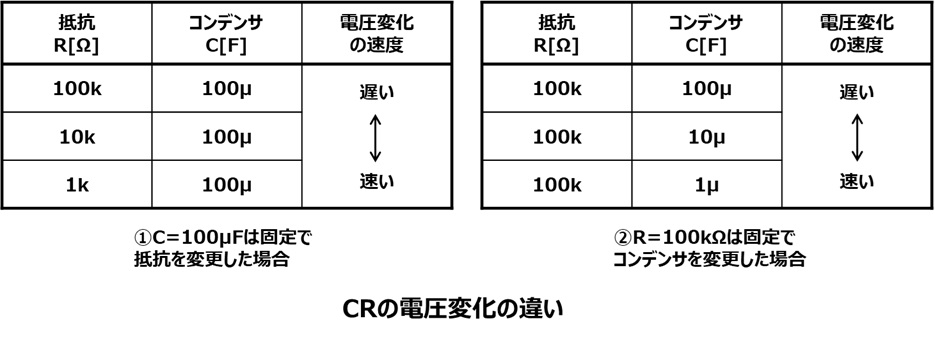
・実験方法6については、電圧の変化がおきませんでした。
■考察
電荷が蓄えられ電圧が変化する速さはCRの積で決まります。
CRの積は時定数と呼びます。実験方法5のそれぞれの組み合わせの時定数を以下の表に示します。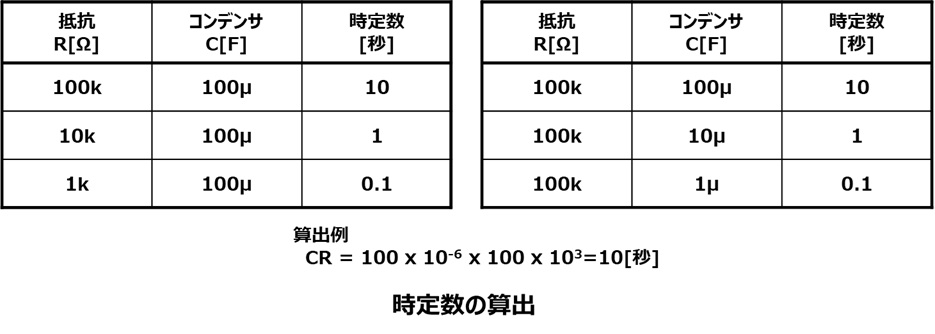
実験方法6の結果では電圧の変化はおきないとしましたが、実際には少しずつ電圧が低下していきます。 それは電圧計側などにもコンデンサから電荷が流出していくためです。
(電圧計には大きな内部抵抗があります。そのため時定数も大きくなりますので、かなりゆっくり電圧低下します)
今回の実験部材
■プッシュスイッチ
プッシュスイッチは、ボタンを押すことで内部の接点を開閉する部品です。
ボタンを押している間は接点が接触し導通、離すと断線するモーメンタリ型と、ボタンを押すことで導通と断線が繰り返されるオルタネート型(保持型)の2種類があります。
いずれも様々な電子機器に使用されています。
スイッチはプッシュスイッチ以外にも動作方式の違いで、スライドスイッチ、ロータリースイッチ、トグルスイッチなど多くの種類があります。
今回の実験
半固定抵抗器と電圧計を使用して簡易的な可変電圧電源をつくり、半固定抵抗を調整することで電圧の変化を観測する実験です。
■実験手順
1.図のようにブレッドボード上に回路をつくります。
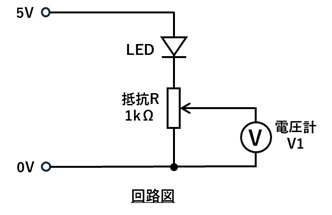

2.電源を投入し、半固定抵抗を左いっぱいに回すと電圧計の値が0Vであることを確認します。
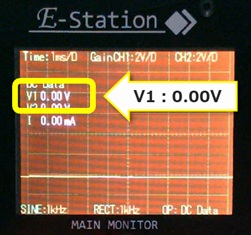
3.半固定抵抗をゆっくり右に回しながら、電圧を可変できることを確認します。
0.1V→0.5V→1V→2V→2.5V→最大(右に回し切り)と電圧計の読みが変化することを観測します。
■測定結果
・ゆっくり右に回すと、電圧が徐々に大きくなり、約3V(3.03V)まで可変できることが分かりました。
0.1V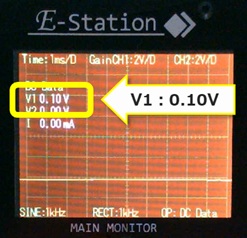
0.5V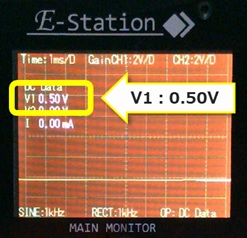
1V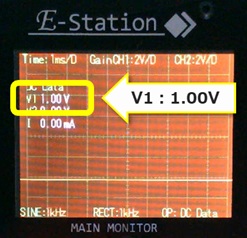
2V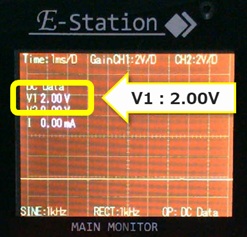
2.5V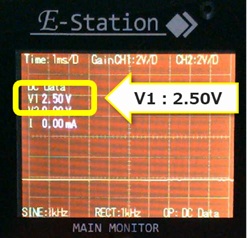
約3V(右に回し切り)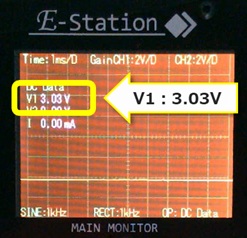
今回は可変電圧電源に負荷をつながないオープン状態で観測しました。今回のような簡易的な電源の場合、その電源電圧は後段につながる負荷の影響を強く受けます。
(電圧が負荷によって変化します)
負荷による変動を小さくしたい場合は、オペアンプをバッファとして入れたり、レギュレータを入れたりして、電圧を安定化させることが一般的です。
今回の実験部材
■半固定抵抗器

※写真は実験に使用した半固定抵抗器と同タイプの100Ω品です
半固定抵抗器はトリマーとも呼ばれます。ドライバーなどを使って軸を回転させることで抵抗値を変化させる構造です。一度調整をすれば固定して使用することを前提としていて、機器の初期設定などに使われます。
一方、抵抗値を変化させる部品としては可変抵抗器(ボリューム)も広く使われています。
可変抵抗器は頻繁に摺動させる前提で設計されており、オーディオアンプの音量調整用途などに使われています。
半固定抵抗も可変抵抗器も摺動させて抵抗値を変化させるという目的から構造は類似していますが、求められる仕様(例えば、耐久性能など)が異なるため、接点構造や材料などに違いがあります。

